Taylor Series

The Taylor Series is an infinite power series.that can be used to approximate a function near a given point.

Definition §

Taylor Series ^definition

Let $f(x)$ be a function that is differentiable infinitely many times. Then, for a point $a$, the Taylor series gives:

$$T(x)=f(a)+f^{\prime }(a)\cdot (x-a)+\frac{f^{\prime \prime }(a)}{2!}\cdot (x-a{)}^2+\dots$$

$$T(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

where $f^{(n)}$ is the $n$-th derivative of $f$ and $n!$ represents the factorial.

Taylor Series (Bivariate) ^definition-bivariate

Let $f(x,y)$ be a bivariate function that is differentiable infinitely many times. Then, for a point $(a,b)$, the Taylor series gives:

$$T_{\infty }(x)=\sum _{n=0}^{\infty }\sum _{m=0}^n\frac{(x-a{)}^m(y-b{)}^{n-m}}{m!(n-m)!}\cdot \frac{{\partial }^{m}f}{\partial x^i\partial y^{k-i}}{|}_{(a,b)}$$

where $f^{(n)}$ is the $n$-th derivative of $f$ and $n!$ represents the factorial.

#todo relate to permutations and pascal triangle.

Taylor Polynomials §

By Taylor’s theorem, we can construct a partial sum, which is, in fact a polynomial (because all partial sums of power series return polynomials). This polynomial is aptly named a Taylor Polynomial, with order $k$

$$T_k(x)=\sum _{n=0}^k\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

The first few Taylor polynomials are given by:

$$T_0(x)=f(a)$$

$$T_1(x)=f(a)+f^{\prime }(a)\cdot (x-a)$$

$$T_2(x)=f(a)+f^{\prime }(a)\cdot (x-a)+\frac{f^{\prime \prime }(a)}{2}(x-a{)}^2$$

Bivariate §

In the bivariate case, the expansions are much more longer due to the binomial-like expansion of the partial derivatives:

$$T_0(x,y)=f(a,b)$$

$$\begin{array}{rl}{T}_1(x,y)& =f(a,b)+\frac{\partial f}{\partial x}{|}_{(a,b)}\cdot (x-a)+\frac{\partial f}{\partial y}{|}_{(a,b)}\cdot (y-b)\\ & =f(a,b)+f_x(a,b)\cdot (x-a)+f_y(a,b)\cdot (y-b)\\ & =f(a,b)+\nabla f(a,b)\cdot [x-a,y-b]\end{array}$$

$$\begin{array}{rl}{T}_2(x,y)& =T_1(x,y)+\frac{{\partial }^{2}f}{\partial x^2}{|}_{(a,b)}\cdot \frac{(x-a{)}^2}{2!}+\frac{{\partial }^{2}f}{\partial x\partial y}{|}_{(a,b)}\cdot \frac{(x-a)(y-b)}{1!1!}+\frac{{\partial }^{2}f}{\partial y^2}{|}_{(a,b)}\cdot \frac{(y-b{)}^2}{2!}\\ & =T_1(x,y)+f_{xx}(a,b)\cdot \frac{(x-a{)}^2}{2!}+f_{xy}(a,b)\cdot \frac{(x-a)(y-b)}{1!1!}+f_{yy}(a,b)\cdot \frac{(y-b{)}^2}{2!}\end{array}$$

Remainder/Error §

Taylor’s theorem also defines an remainder function $R_k(x)$.

The error is then defined to be $|R_k(x)|$

$$R_k(x,y)=\sum _{n=0}^k\frac{f^{(n)}(a+\xi (x-a))}{n!}(x-a{)}^n$$

Bivariate Remainder §

The explicit formula for the Taylor remainder in a bivariate case is (for a function $f(x,y)$ near the point $(a,b)$)

$$R_k(x,y)=\sum _{n=0}^{k+1}\frac{(x-a{)}^n(y-b{)}^{k+1-n}}{n!(k+1-n)!}\cdot {\frac{{\partial }^{k+1}f}{\partial x^n\partial y^{n+1-k}}|}_{(a+\xi (x-a),b+\xi (y-b))}$$

For some $0<\xi <1$

For the first few Taylor polynomials:

$$R_1(x,y)=\frac{(x-a{)}^2}{2!}\cdot f_{xx}(p)+\frac{(y-b{)}^2}{2!}\cdot f_{yy}(p)+\frac{(x-a)(y-b)}{1!1!}\cdot f_{xy}(p)$$

where $p=(a+\xi (x-a),b+\xi (y-b))$ and $\xi \in (0,1)$

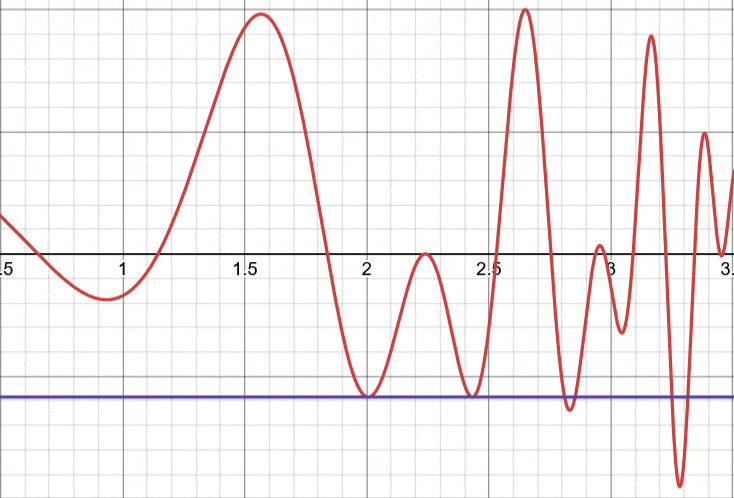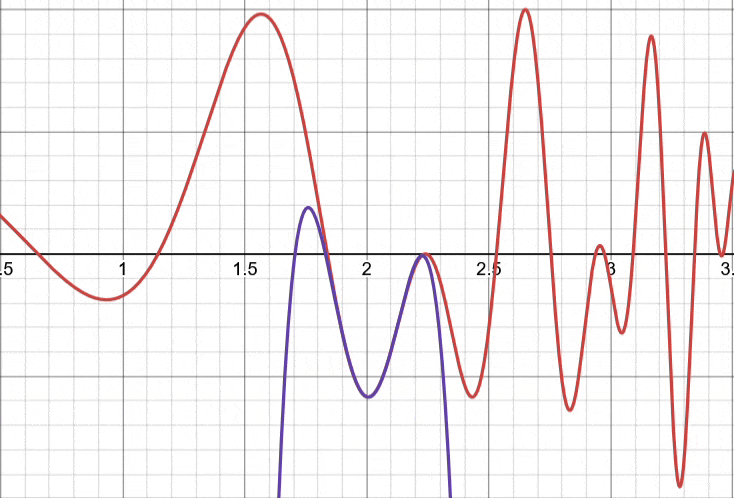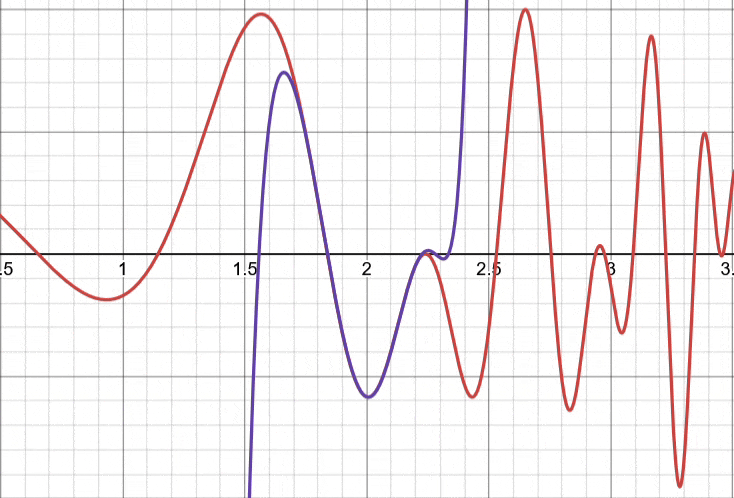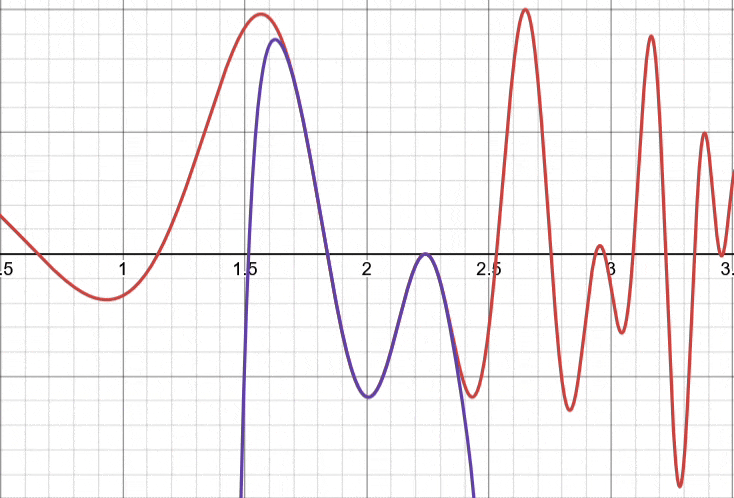
Taylor’s Theorem §

Taylor's Theorem ^t1

Taylor’s theorem states that, for any function that is differentiable $k$ times, it can be well-approximated by the partial sum near some point $a$

$$f(x)\approx T_k(x)=\sum _{n=0}^k\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

if, and only if the remainder $R_k(x)$ approaches 0 as $k\to \infty$.

$$\underset{k\to \infty }{\lim }{R}_k(x)=0⟺\underset{k\to \infty }{\lim }\sum _{n=0}^k\frac{f^{(n)}(a+\xi (x-a))}{n!}(x-a{)}^n=0$$

Explanation §

#todo use video resource!

#todo Connection to Hessian matrix.

Examples §

1: Second-order Taylor polynomial

Find the second-order Taylor polynomial $T_2$ for the function $f(x,y)=e^{xy}$ near the point $(1,0)$. Hence, approximate $e^{0.11}$

Solution $T_2$ is given by:

The formula for the second-order Taylor polynomial

$$\begin{array}{rl}{T}_2(x,y)& =T_1(x,y)+\frac{{\partial }^{2}f}{\partial x^2}{|}_{(a,b)}\cdot \frac{(x-a{)}^2}{2!}+\frac{{\partial }^{2}f}{\partial x\partial y}{|}_{(a,b)}\cdot \frac{(x-a)(y-b)}{1!1!}+\frac{{\partial }^{2}f}{\partial y^2}{|}_{(a,b)}\cdot \frac{(y-b{)}^2}{2!}\\ & =T_1(x,y)+f_{xx}(a,b)\cdot \frac{(x-a{)}^2}{2!}+f_{xy}(a,b)\cdot \frac{(x-a)(y-b)}{1!1!}+f_{yy}(a,b)\cdot \frac{(y-b{)}^2}{2!}\end{array}$$

We can use this explicit formula to obtain

$$\begin{array}{rl}{T}_2(x,y)& =f(1,0)+f_x(1,0)\cdot (x-1)+f_y(1,0)\cdot (y-0)\\ & +f_{xx}(1,0)\cdot \frac{(x-1{)}^2}{2!}+f_{xy}(1,0)\cdot \frac{(x-1)(y-0)}{1!1!}+f_{yy}(1,0)\cdot \frac{(y-0{)}^2}{2!}\\ & =e^0+y\cdot e^{xy}{|}_{(1,0)}\cdot (x-1)+x\cdot e^{xy}{|}_{(1,0)}\cdot y+y^2\cdot e^{xy}{|}_{(1,0)}\cdot \frac{(x-1{)}^2}{2}\\ & +(e^{xy}+xy\cdot e^{xy}){|}_{(1,0)}\cdot \frac{y(x-1)}{1}+x^2\cdot e^{xy}{|}_{(1,0)}\cdot \frac{(y{)}^2}{2}\\ & =1+0+y+0+y(x-1)+\frac{y^2}{2}=1+y+y(x-1)+\frac{y^2}{2}\\ & =1+xy+\frac{y^2}{2}\end{array}$$

Now, we need to find a combination $(x,y)$ that is close to the point $(1,0)$ such that $e^{xy}=e^{0.11}$. Take $(x,y)=(1.1,0.1)$. Then $e^{xy}=e^{11/10\cdot 1/10}=e^{0.11}$ Using the Taylor polynomial, we get:

$$T_2(1.1,0.1)=1+1.1\cdot 0.1+\frac{0.1^2}{2}=1.115$$

Compare it to the actual value of the function, $f(1.1,0.1)=e^{0.11}=1.116$

2: Taylor Polynomial of a harmonic function and error-bounding. ^e2

Find the 2nd-order Taylor polynomial for $f(x,y)=\sin (x+2y)$ near the point $(0,0)$. Also, find an upper bound for the error if $|x|<0.1$ and $|y|<0.1$.

Solution $T_1$ (since $T_2$ is just an extension of $T_1$):

We can start by finding

$$\begin{array}{rl}{T}_1(x,y)& =f(0,0)+f_x(0,0)\cdot (x-0)+f_y(0,0)\cdot (y-0)\\ & =0+\cos (0)\cdot x+2\cos (0)\cdot y\\ & =x+2y\end{array}$$

Then, $T_2$ is given by:

$$T_2(x,y)=T_1(x,y)+f_{xx}(0,0)\cdot \frac{(x-0{)}^2}{2!}+f_{yy}(0,0)\cdot \frac{(y-0{)}^2}{2!}+f_{xy}(0,0)\cdot \frac{(x-0)\cdot (y-0)}{1!1!}$$

Before we compute this value, recall that the second derivative of $\sin$ is $-\sin$. Since we are inputting values $x=0$ and $y=0$, we know all the second derivatives become 0!

So:

$$T_2(x,y)=T_1(x,y)+{\cancel{f_{xx}(0,0)\cdot \frac{(x-0{)}^2}{2!}}}^0+{\cancel{f_{yy}(0,0)\cdot \frac{(y-0{)}^2}{2!}}}^0+{\cancel{f_{xy}(0,0)\cdot \frac{(x-0)\cdot (y-0)}{1!1!}}}^0$$

That is:

$$T_2(x,y)=x+2y$$

Using the formula for the remainder, we have:

$$\begin{array}{rl}{R}_2(x,y)& =\frac{{\partial }^{3}f}{\partial x^3}(p)\cdot \frac{(x-0{)}^3}{3!}+\frac{{\partial }^{3}f}{\partial y^3}(p)\cdot \frac{(y-0{)}^3}{3!}+\frac{{\partial }^{3}f}{\partial x^2\partial y}\cdot \frac{(x-0{)}^2\cdot (y-0)}{2!1!}+\frac{{\partial }^{3}f}{\partial x\partial y^2}\cdot \frac{(x-0)\cdot (y-0{)}^2}{1!2!}\\ & =\frac{{\partial }^{3}f}{\partial x^3}(p)\cdot \frac{x^3}{6}+\frac{{\partial }^{3}f}{\partial y^3}(p)\cdot \frac{y^3}{6}+\frac{{\partial }^{3}f}{\partial x^2\partial y}\cdot \frac{x^{2}y}{2}+\frac{{\partial }^{3}f}{\partial x\partial y^2}\cdot \frac{x{y}^2}{2}\end{array}$$

where $p=(a+\xi (x-a),b+\xi (y-b))=(\xi x,\xi y)$ and $0<\xi <1$.

Recall that the third derivative of $\sin$ is $-\cos$.

$$\begin{array}{rl}{R}_2(x,y)& =-\frac{x^3}{6}\cos (\xi x+2\xi y)-\frac{8y^3}{6}\cos (\xi x+2\xi y)-x^{2}y\cos (\xi x+2\xi y)-2x{y}^2\cos (\xi x+2\xi y)\\ & =-\frac{1}{6}\cos (\xi x+2\xi y)(x^3+6x^{2}y+12x{y}^2+8y^3)\\ & =-\frac{1}{6}\cos (\xi x+2\xi y)(x+2y{)}^3\end{array}\text{\hspace{1em}(Cubic expansion)}$$

The error is then given by:

$$|R_2(x,y)|=\frac{1}{6}|\cos (\xi x+2\xi y)||(x+2y{)}^3|$$

Since we know that $\cos$ is bounded by $-1\le \cos (x)\le 1$, we have $0\le |\cos (x)|\le 1$

Thus:

$$\begin{array}{rl}|R_2(x,y)|& \le \frac{1}{6}|(x+2y{)}^3|\\ & \le \frac{1}{6}(|x{|}^3+6|x{|}^2|y|+12|x||y{|}^2+8|y{|}^3)\end{array}\text{\hspace{1em}(Triangle Inequality)}$$

See cauchy-schwarz inequality for an explanation of the triangle inequality used. Since we are given $|x|<0.1$ and $|y|<0.1$, we have:

$$\begin{array}{rl}|R_2(x,y)|& <\frac{1}{6}(0.1^3+6\cdot 0.1^3+12\cdot 0.1^3+8\cdot 0.1^3)\\ & <\frac{1}{6}(27\cdot 0.1^3)=0.0045\end{array}$$

Thus, the upper bound for the error is provided above.

3: Using Taylor approximations for solving limits

Evaluate the limit:

$$\underset{(x,y)\to (0,0)}{\lim }\left(\frac{\sin (x+2y)}{x+2y}\right)$$

Solution example 2, we know that as $(x,y)\to (0,0)$, our function can be well-approximated by the Taylor polynomial $x+2y$.

From

That is, we can let:

$$\begin{array}{rl}\sin (x+2y)& =T_2(x,y)+R_2(x,y)\\ & =x+2y-\frac{1}{6}\cos (\xi x+2\xi y)(x+2y{)}^3\end{array}\text{\hspace{1em}(0<ξ<1)}$$

Then, our limit becomes:

$$\begin{array}{rl}\underset{(x,y)\to (0,0)}{\lim }\left(\frac{\cancel{x+2y}+R_2(x,y)}{\cancel{x+2y}}\right)& =\underset{(x,y)\to (0,0)}{\lim }\left(1+\frac{R_2(x,y)}{x+2y}\right)\\ & =\underset{(x,y)\to (0,0)}{\lim }(1-\frac{1}{6}\cos (\xi x+2\xi y)(x+2y{)}^2)\end{array}$$

By continuity theorems, we have:

$$\underset{(x,y)\to (0,0)}{\lim }(1-\frac{1}{6}\cdot 0)=1$$

Thus, we used the Taylor approximation to simplify and solve the limit.

Applications §

• The first-order Taylor polynomial $T_1$ returns the linear approximation of a function
  • $T_2$ returns the quadratic approximation
  • $T_3$ returns the cubic approximation
  • and so on…

Resources §

• The Subtle Reason Taylor Series Work | Smooth vs. Analytic Functions - Morphocular