Continuity (Calculus)

A function is continuous if it has no ‘breaks’ along its curve. Continuity is a very important property, as functions are only differentiable if they are continuous. More formally, continuity is defined by limits

Definition §

Continuity ^definition

Let $f$ be a real-valued function (i.e. $f:D\subseteq \mathbb{R}\to \mathbb{R}$). Then, for some point $a$:

$$\text{f is continuous at a}\leftrightarrow \underset{x\to a}{\lim }f(x)=f(a)$$

That is, the limit of $f$ exists and is equal to $f(a)$

Bivariate Continuity §

Continuity (Bivariate) ^definition-bivariate

Let $f$ be a bivariate function (i.e. $f:D\subseteq {\mathbb{R}}^2\to \mathbb{R}$). Then, for some point $(a,b)$:

$$\text{f is continuous at (a,b)}\leftrightarrow \underset{(x,y)\to (a,b)}{\lim }f(x,y)=f(a,b)$$

This is essentially the same as the univariate case.

Continuous Everywhere Functions §

The following function types are always continuous along their entire domain i.e. continuous everywhere:

• Polynomials
• trigonometric functions: sin x, cos x, tan x, sec x, cosec x, cot x, arcsin x, arccos x, arctan x
• exponential functions: $a^x,a>0$

• logarithm functions: ${\log }_a(x),x>0$
• $n$th root functions: $\sqrt[n]{x},n>1$
• absolute value function: |x|
• Hyperbolic functions

Theorems §

T1: Continuity is preserved under certain operations ^t1

Let $f$ and $g$ be continuous functions at $x=a$, then the following functions are continuous (at $x=a$):

1. $f+g$
2. $c\cdot f$ where $c$ is a constant
3. $f\times g$,
4. $\frac{f}{g}$ if $g(a)\ne 0$

This also applies to continuous everywhere functions

T2: Function composition preserves continuity

If $f$ is continuous at $x=a$ and $g$ is continuous at $x=f(a)$, then the function composition $f\circ g$ is continuous at $x=a$.

This theorem is very useful in finding continuity of complex functions by breaking them down into simpler functions (decomposing) and then checking which of them are continuous everywhere

T3: Continuity of Limits ^t3

If a function can be represented as $f(g(x))$ and ${\lim }_{x\to a}g(x)=b$. Then, if $f$ is continuous at $b$.

$$\underset{x\to a}{\lim }f(g(x))=f(\underset{x\to a}{\lim }g(x))=f(b)$$

This is very, very useful to break down limits, since we can simplify complex functions into those that are continuous everywhere, and then apply this theorem.

T4: Continuity of Partial Derivatives ^t4

If a function’s partial derivatives $\frac{\partial f}{\partial x_i}$ are continuous, then their order can be swapped.

$$\frac{\partial f}{\partial x}\text{ and }\frac{\partial f}{\partial y}\text{ are continuous}⟹\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{{\partial }^{2}f}{\partial y\partial x}$$

Examples §

Bivariate Examples §

1: Discontinuity

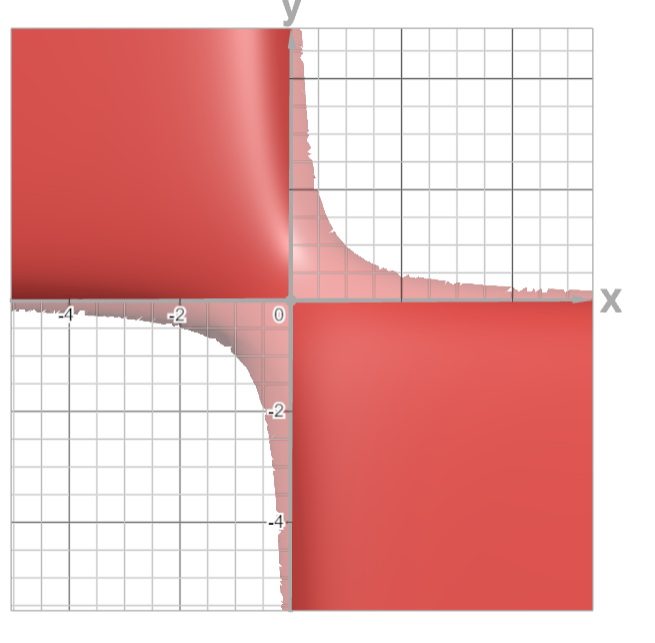
Is the function $f(x)=\frac{x^2}{x^2+y^2}$ continuous at (0,0)?

Solution $f$ is undefined at $(0,0)$ because it would result in a division by zero, which is undefined. Hence, since we know that the function value does not exist, it could never be equal to the limit, and we can stop here instead of checking the limit as well. $f$ is discontinuous at the point $(0,0)$.

This is actually very easy to solve. We know that

Visuals

\usepackage{pgfplots}
\pgfplotsset{width=20cm,compat=1.16}
\begin{document}

\begin{tikzpicture}
\begin{axis}[colormap/bluered]
\addplot3[
	mesh,
	samples=30,
	domain=-3:3
]
{x^2/(x^2 + y^2)};
\end{axis}
\end{tikzpicture}

\end{document}

1: Bivariate Continuity

Where is $f(x,y)=\log (1-xy)$ continuous?

Solution $f$ can be expressed as a composition of functions $(h\circ g)(x,y)=h(g(x,y))$ where:

• $h(z)=\log (z)$ is continuous everywhere (logarithm) over the domain $z>>0$
• $g(x,y)=1-xy$ is continuous everywhere (polynomial) over the domain $(x,y)\in {\mathbb{R}}^2$

For the function composition to be valid, we need to restrict $\text{ran}(g)=\text{dom}(h)$: $1-xy>>0⟹y<\frac{1}{x}$. Then by continuity of composition, we have:

$$f(x,y)\text{ is continuous for }D=\{(x,y)\in {\mathbb{R}}^2:y<\frac{1}{x}\}$$

We can see this visually: #TODO ALSO FOR $y>>\frac{1}{x}$ if $x<0$

Visuals

\usepackage{pgfplots}
\pgfplotsset{width=15cm,compat=1.16}
 \begin{document}
 \begin{tikzpicture}
 \begin{axis}[colormap/bluered, view = {60}{30}]
 
 \addplot3[
 	mesh,
 	samples=30,
 	domain=-0.8:0.8
 ]
 {ln(1-(x*y))};
 \end{axis};
 

 
 \end{tikzpicture}
 
 \end{document}

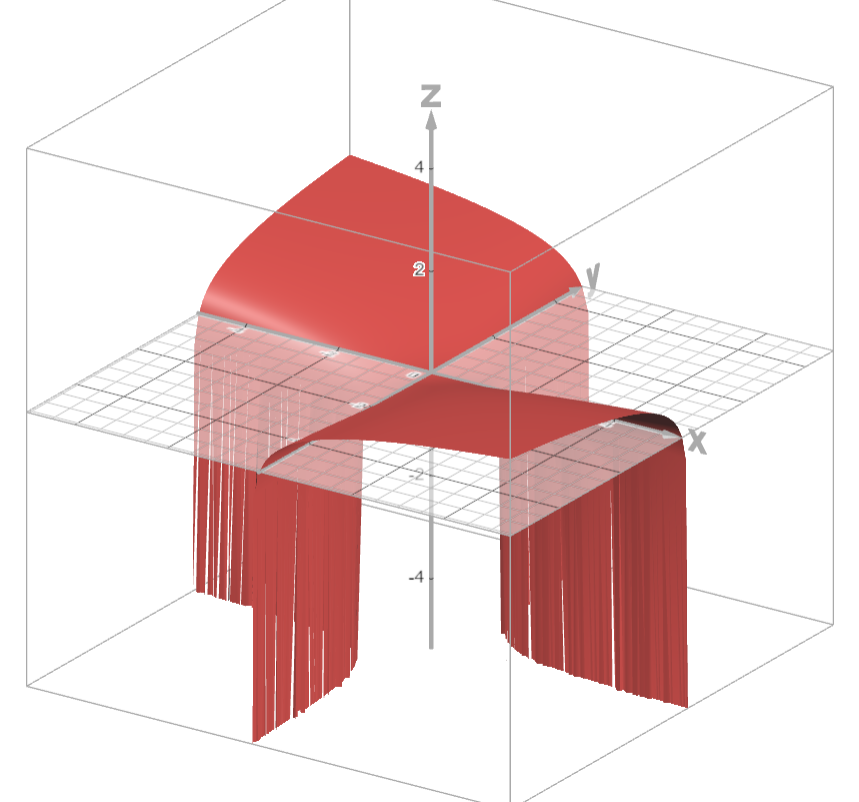
2: Continuity of a bivariate piecewise function

Where is the following function continuous?

$$f(x,y)=\{\begin{array}{ll}\frac{x^2}{\sqrt{x^2+y^2}},& (x,y)\ne (0,0)\\ 0,& (x,y)=(0,0)\end{array}$$

Solution

Because this function is defined differently at different locations (due to being piecewise), we need to evaluate it in a case-by-case basis:

1. $(x,y)\ne (0,0)$

• $f(x,y)$ can be expressed as the quotient of functions $f(x,y)=\frac{g(x,y)}{h(x,y)}$ where $g(x,y)=x^2$ and $h(x,y)=\sqrt{x^2+y^2}$.
• $g(x,y)$ is continuous everywhere over its domain (due to being a polynomial function)
• $h(x,y)$ is a composition: $h(x,y)=\alpha \circ \beta (x,y)$ where $\alpha (z)=\sqrt{z}$ and $\beta (x,y)=x^2+y^2$
  • $\alpha$ is continuous everywhere (square root functions are continuous)
  • $\beta$ is the sum of polynomial functions, and is hence continuous everywhere.
  • By theorem 2, $h$ is continuous everywhere over its domain.
• Hence, $f(x,y)$ is continuous everywhere for $(x,y)\ne (0,0)$ (due to theorem 1)

1. By definition of the function, we know that $f(0,0)=0$. It can be shown that ${\lim }_{(x,y)\to (0,0)}f(x,y)=0$. Hence since the limit is equal to the function value, $f$ is continuous at $(0,0)$

Hence, $f$ is continuous for all $(x,y)\in {\mathbb{R}}^2$