Partial Fraction Decomposition

Partial fraction decomposition involves representing a fraction consisting of polynomials as a sum of a quotient polynomial, and another fraction. This technique is useful in integration.

Definition §

Let $f(x)$ and $g(x)$ be two polynomials, where the degree of $f$ is greater than that of $g$. Then we can use polynomial long division to obtain:

$$\frac{f(x)}{g(x)}=Q(x)+\frac{R(x)}{g(x)}$$

• $Q(x)$ is the quotient polynomial
• $R(x)$ is the remainder polynomial. The degree of $R(x)$ is always less than $g(x)$.

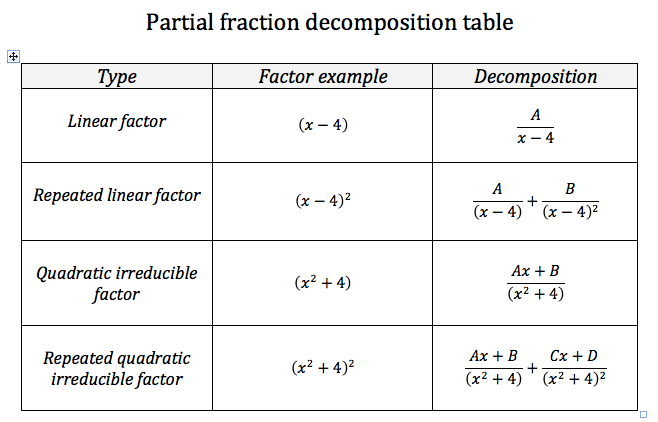
The remainder polynomial can then further be decomposed into partial fractions, based on the form of $g(x)$:

Denominator Form ($g(x)$)	Also called	Decomposition
$(ax+b)\times (cx+d)\times \dots$	Linear Factors	$\frac{A}{ax+b}+\frac{B}{cx+d}+\dots$
$(ax+b{)}^2$	Repeated Linear Factor	$\frac{A}{ax+b}+\frac{B}{(ax+b{)}^2}$
$(ax+b{)}^n$	Repeated Linear Factor	$\frac{A}{ax+b}+\frac{B}{(ax+b{)}^2}$ $+\frac{C}{(ax+b{)}^3}+\dots \frac{N}{(ax+b{)}^n}$
$(a{x}^2+bx+c)$	Irreducible Quadratic Factor	$\frac{Ax+B}{a{x}^2+bx+c}$
$(a{x}^n+b{x}^{n-1}+c{x}^{n-2}+\cdots +n)$	Irreducible Nth Factor	$\frac{A{x}^{n-1}+B{x}^{n-2}+\dots N}{a{x}^n+b{x}^{n-1}+c{x}^{n-2}+n}$

Examples §