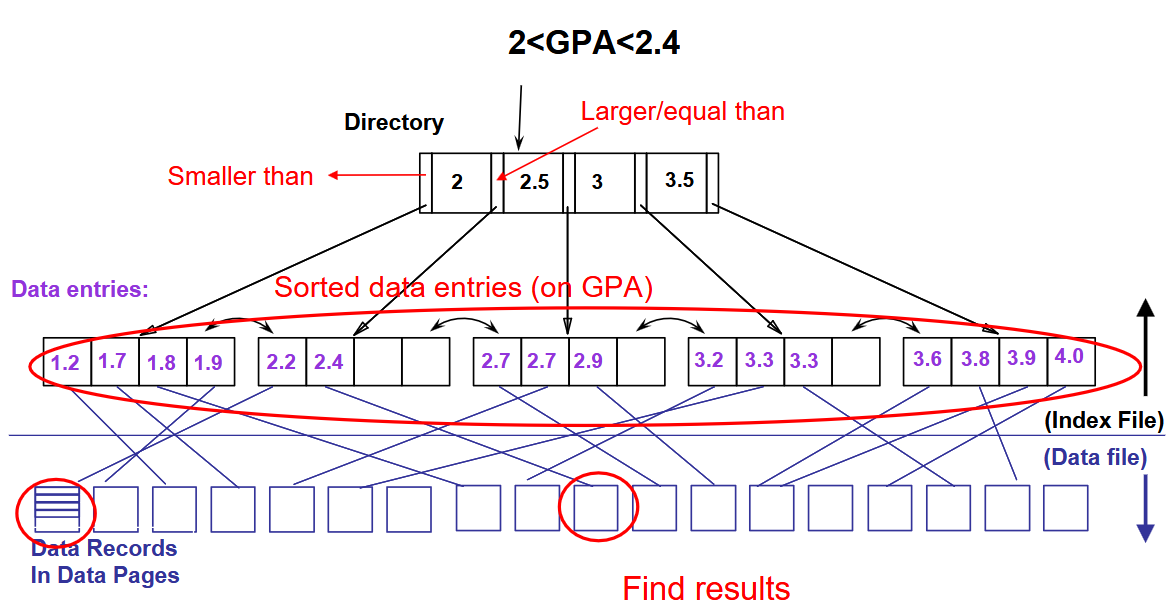
An index is a data structure built on top of data pages used for efficient search. The index is built over specific fields called search key fields. The index can built on any attribute. The index speeds up selections on the selected search key fields. Indexes can either be generated via a B+ Tree (tree-based) or a hash table (hash-based)
- Any subset of the fields of a relation can be search key for an index of the relation
- If an index has multiple search key fields, it is said to have composite search keys.
- A search key is not the same as a relational key, i.e. it does not need to be unique
Tree-based
In most cases, the indexes are built using a tree-based approach (#tosee why?) using a data structure known as a B+ tree.
%%🖋 Edit in Excalidraw, and the light exported image%%
Clustered & Unclustered
If the order of data records is the same as the order of index data entries, then the index is called clustered index. Else, the index can be treated as unclustered
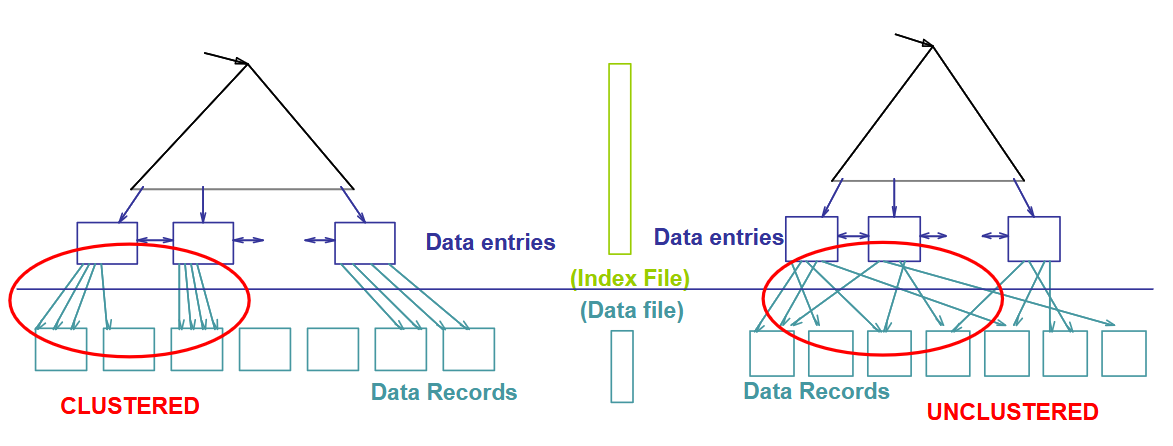
- A data file can have a clustered index on at most one search key combination (i.e. we cannot have multiple clustered indexes over a single table)
- Cost of retrieving data records through index varies greatly based on whether index is clustered (cheaper for clustered).
- Clustered indexes are more expensive to maintain (require file reorganization), but are really efficient for range search.
(Approximated) cost of retrieving records found in range scan:
- Clustered: cost ≈ # pages in data file with matching records
- Unclustered: cost ≈ # of matching index data entries (data records)
Primary & Secondary
Primary index includes the table’s primary key. Similarly, a secondary index is any other non-primary index.
- Primary index never contains duplicates
- Secondary index may contain duplicate
Hash-based
An alternative to the B+ tree is using a Hash Table (i.e. a hashing function) to map attributes in buckets.
- Represents index as a collection of buckets. Hash function maps the search key to the corresponding bucket.
- Good for equality selections