Geometric Series

A geometric series is a series in which future terms are generated by the multiplication of a common factor, $r$. It is always in the form:

$$\sum _{n=1}^{\infty }a\times r^{n-1}=ar+a{r}^2+a{r}^3+\dots a{r}^{n-1}$$

where $a\in \mathbb{R}\backslash \{0\}$ and $r\in \mathbb{R}$

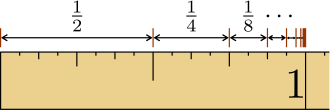
The series converges if $|r|<1$ and diverges if $|r|\ge 1$. Since we are repeatedly multiplying by a number smaller than 1, we are essentially reducing the value of future terms, and hence the final sum converges into a value. If $|r|<1$ then:

$$\sum _{n=0}^{\infty }a{r}^n=\frac{a}{1-r}$$

General Formula §

This formula is obtained by the general formula for geometric series: ${\sum }_{k=0}^{n}a{r}^k=\frac{a(1-r^{n+1})}{1-r}$

Examples §

1. $a_n=\frac{1}{2^n}$: $s_n=\frac{2^n-1}{2^n}=1-\frac{1}{2^n}$

${\sum }_{n=1}^{\infty }{a}_n$ converges to $1$ ($a=1/2,r=1/2$)