Function (Maths)

A function is some process that transforms elements from one set to another.

%%🖋 Edit in Excalidraw, and the dark exported image%%

Definition §

Function ^definition

A function $f$ is some mapping that takes values from a set $X$ and transforms/maps them into values in another set $Y$. This is notated as:

$$f:X\to Y$$

• $X$ is known as the domain of the function. $\text{dom}(f)=X$
• $Y$ is known as the codomain of the function

This also means elements $y\in Y$ can be represented as a function of elements $x\in X$:

$$y=f(x)$$

• $y$ is called the image of $x$
• $x$ is the argument of $f$

Because $f$ is defined on the domain $X$, every element of $X$ must be mapped to some value in $Y$.

#todo unify function image and linear algebra image

Range §

Range (of a function) ^definition-range

The range of a function $f$ is a subset of the codomain that contains exactly all the images of the domain. It is defined to be:

$$\text{ran}(f)=\{y\in Y:\exists x\in X,y=f(x)\}$$

That is, it contains all the points that are the result of mapping the domain with $f$. %%🖋 Edit in Excalidraw, and the dark exported image%%

Arity §

Arity ^definition-arity

The arity of a function, $f$, is the number of arguments it takes or equivalently the dimension of its domain $X$. That is, if we have:

$$f:X^n\to Y$$

then $f$ is an $n$-ary function. Some unique cases are:

• $n=0$: Nullary/constant function ($y=c$)
• $n=1$: Unary function ($y=f(x)$)
• $n=2$: Binary Function ($z=f(x,y)$)

Properties §

Injective §

A function is said to be injective if it is one-to-one, i.e. there is only one value in $X$ that maps to $Y$. More precisely:

$$f\text{ is injective}\leftrightarrow f(x)=f(y)\to x=y$$

600 $f$ is injective in the drawing above, because even though not everything is mapped, there is only one, unique element in $X$ that maps to another unique element in $Y$. $g$ is not injective, because both $g(a)$ and $g(d)$ equal $4$.

Graphically, if the function is a real that can be mapped on the Cartesian Plane, i.e. $f:\mathbb{R}\to \mathbb{R},x=f(y)$, then $f$ is injective if a horizontal line intersecting each value of y does not have multiple intersections with the function.

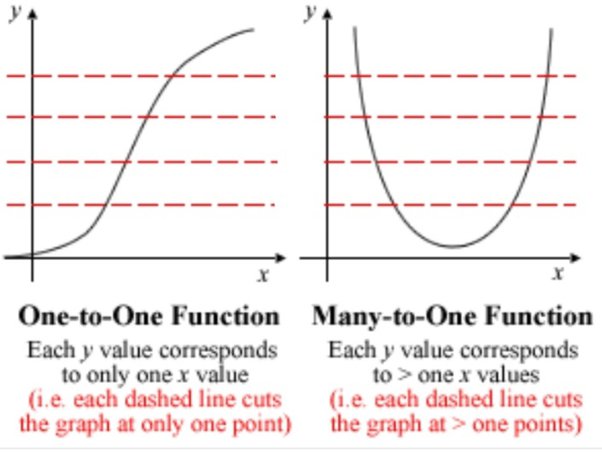
This one-to-one notion can be proved via linear algebra using the definition of injectivity in linear transformations. See: http://thejuniverse.org/PUBLIC/LinearAlgebra/MATH-232/Unit.8/Presentation.1/Section7B/oneone.html

Surjective §

A function is surjective if every element of it’s codomain has at least one corresponding element in the domain, i.e. for every element in $Y$, there exists an element in $X$ such that $f(x)=y$. More precisely:

$$f\text{ is surjective}\leftrightarrow \forall y\in Y,\exists x\in X|f(x)=y$$

600 Here, $f$ is non-surjective because the element $4\in Y$ has no corresponding value in $X$. $g$, however, is surjective, because every element in $Y$ has one or more corresponding elements in $X$.

Bijective §

A bijective function is one that is both injective and surjective. In other words, every element in $Y$ must have one corresponding element in $X$.

Function - Maths _1.excalidraw

Even §

Odd §

Scalar Function §

Vector Function §