Symmetry is an important feature that connects Electric Fields to Charge Distributions. In essence, the symmetry of a field must match with that of the associate charge distribution.
If we had an charge distribution that was symmetrical in rotation, reflection and translation, then, by definition of symmetry, rotating, reflecting and translating the object (on certain axes) should not change it in anyway. Because the electric field stems from these charge distributions, it too should follow the same symmetry.
Fundamental Symmetries
Objects that resemble these fundamental symmetries are usually perfectly symmetrical with respect to translation, rotation and reflection (in certain axes). As such, their electric fields are also symmetrical, and easy to obtain. These shapes can be used to model much more complex surfaces.
There are 3 fundamental symmetries:
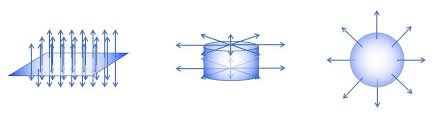
- Plane Symmetry: Essentially what an Plane of Charge is, has an electric field that is constant and is perpendicular to the plane at all times.
- Cylindrical Symmetry: See Charged Cylinder with Infinite Length for mathematical derivation. The electric field is perpendicular to the curved surface of the cylinder, and is zero at the ‘caps’ or circle
- Spherical Symmetry: The field is always radially away/towards the centre of the sphere.
These fundamental symmetries can be used as Gaussian Surfaces in order to use Gauss’ Law to determine electric fields easily.