Solenoid

A solenoid is tightly coiled helical arrangement of a wire that maximises the Magnetic Field that goes through it’s loops when a current is flowing through it. They operate in a similar principle to Capacitor (Physics)s*, in the sense that they generate a uniform, straight field.

*See Inductor (Physics)s for the magnetic equivalent to capacitors.

Magnetic Field §

Note Magnetic Field of a Solenoid

\vec{B} = \mu_{0} nI = \mu_{0} \dfrac{NI}{l}

>[!terms]- >* $\vec{B}$ = [Magnetic Field](Magnetic%20Field.md) (in $\text{T}$) >* $n$ = Turns per unit length ($\text{1/m}$) >* $N$ = Total turns of wire ($\text{unitless}$) >* $l$ = Length of solenoid (in $\text{m}$) >* $I$ = [Current](Current.md) flowing through solenoid (in $\text{A}$)

Relation to a Magnet §

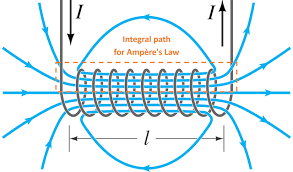
Derivation (using Ampère’s Law) §

Assume we have a solenoid with a current $I$ flowing through each of the loops inside it, with $N$ loops and a total length of $L$. Also assume the magnetic field is only flowing between the solenoid (due to superposition)#todo

Using Ampère’s Law:

$$\oint \vec{B}\cdot d\vec{l}=I_{enc}{\mu }_0$$

We know in the amperian loop, certain sections (in red) are perpendicular to the magnetic field, so $d\vec{l}\cdot \vec{B}=0$ (i.e. does not contribute).

We have only two sections of the loop parallel to the field, but in one side (outside the solenoid), $\vec{B}=0$, so:

$$\oint \vec{B}\cdot d\vec{l}=\oint B\text{d}l=Bl$$

The total current, $I_{enc}$, flowing through the amperian loop is given by the number of loops. Because through each loop, the current flowing is the same, and not divided up:

$$I_{enc}=N_{loops}\times I$$

Combining the two:

$$Bl=NI{\mu }_0$$

$$B={\mu }_{0}I\times \frac{N}{l}$$

If we define $n$ to be the ratio of number of wire loops to the length of the solenoid, we get:

$$B={\mu }_{0}In$$

Which gives our formula