PageRank is a recursive algorithm that ranks nodes(pages) in a directed graph(web). It works on the principal that a page is important if important pages link to it. This definition is circular, so a base case is created, where every page is equally important.
Formula
PR(A_0) = \frac{1}{|V|}$$
* B and C are nodes that point to A.
* $d$ = Damping Constant (0.85 in most cases). It represents that chance that a user will click another link in the page he was currently on, instead of just searching for a new page
* $L(n)$ = The out degree of n i.e. the number of outgoing edges. **If the node is a sink node, it is converted into a source node, by adding edges to every node (including itself!)**
* $\frac{1-d}{|V|}$ represents the surfer probability, the chance that a random person outside the page finds it
### Example
Consider the network shown below, with 4 nodes:
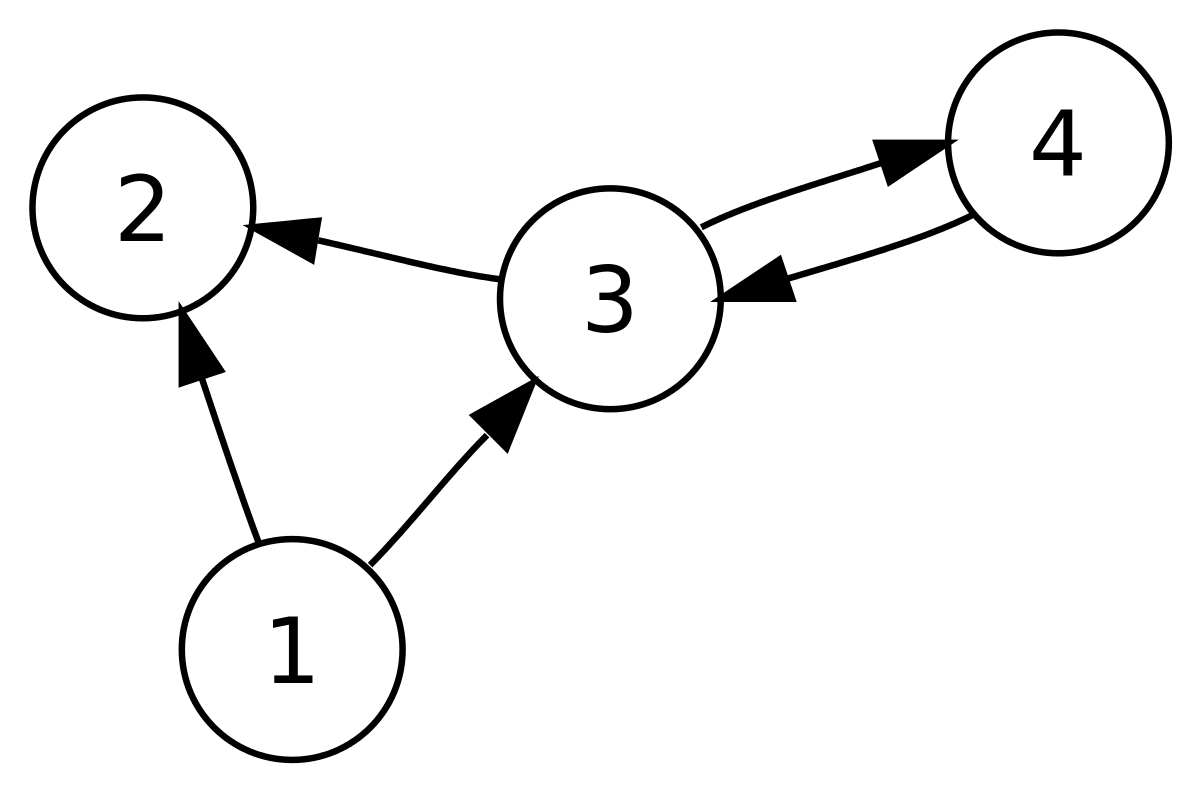
The PageRank formula and values would be as follows:
| Node | Formula - PR(Node) |
| ---- | ------------------------------------------------------------------------------------------ |
| 1 | $\frac{1-0.85}{4} + 0.85( \frac{PR(2)}{4})$ |
| 2 | $\frac{1-0.85}{4} + 0.85\left( \frac{PR(1)}{2} + \frac{PR(3)}{2} \right)$ |
| 3 | $\frac{1-0.85}{4} + 0.85\left( \frac{PR(1)}{2}+ \frac{PR(2)}{4} + \frac{PR(4)}{1}\right)$ |
| 4 | $\frac{1-0.85}{4} + 0.85\left( \frac{PR(2)}{4} + \frac{PR(3)}{1} \right)$ |
| Iteration | 1 | 2 | 3 | 4 |
| --------- | ---- | ---- | ---- | ---- |
| 0 | 0.25 | 0.25 | 0.25 | 0.25 |
| 1 | 0.09 | 0.30 | 0.41 | 0.20 |
| 2 | 0.10 | 0.31 | 0.31 | 0.28 |
| 3 | 0.10 | 0.28 | 0.38 | 0.24 |
| 4 | 0.10 | 0.30 | 0.34 | 0.26 |
| 10 | 0.10 | 0.29 | 0.36 | 0.25 |
As you can see, node 3 is considered most important, with 2 being second, 4 being 3rd and 1 being last.
### Pseudocode
```
Algorithm PageRank(G):
d ← 0.85
For each node n in G do:
PR(n) ← 1/|V| #PR is be a node attribute, but this style shows recursion better
If n.outdegree = 0 then:
For each node n2 in G do:
Add edge n-n2 to G
End do
End if
End do
Repeat until convergence: #Convergence can mean 100,1000,etc.
For each node n in G:
total ← 0
For each incoming node to n:
total ← total + PR(incoming)/incoming.outdegree
End do
PR(n) ← (1-d)/|V| + d*(total)
End do
End do
End Algorithm
```
### Implementation
