Function - Maths

A function is some process that transforms elements from one set to another.

A function, $f$, which maps a set, $X$ onto another set, $Y$ can be notated as:

$$f:X\to Y$$

Properties §

Injective §

A function is said to be injective if it is one-to-one, i.e. there is only one value in $X$ that maps to $Y$. More precisely:

$$f\text{ is injective}⟺f(x)=f(y)⟹x=y$$

600 $f$ is injective in the drawing above, because even though not everything is mapped, there is only one, unique element in $X$ that maps to another unique element in $Y$. $g$ is not injective, because both $g(a)$ and $g(d)$ equal $4$.

Graphically, if the function is a real that can be mapped on the Cartesian Plane, i.e. $f:\mathbb{R}\to \mathbb{R},x=f(y)$, then $f$ is injective if a horizontal line intersecting each value of y does not have multiple intersections with the function.

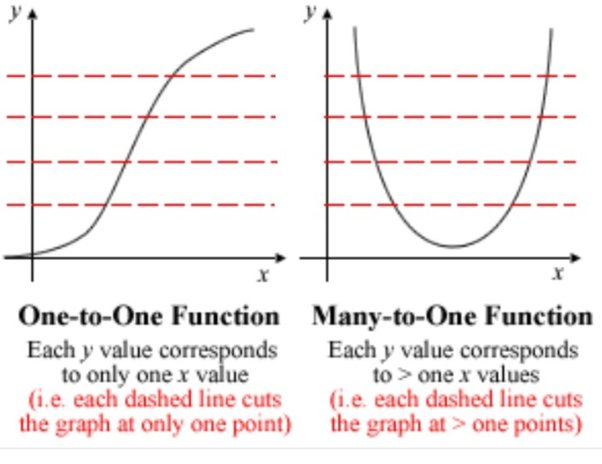
Surjective §

A function is surjective if every element of it’s codomain has at least one corresponding element in the domain, i.e. for every element in $Y$, there exists an element in $X$ such that $f(x)=y$. More precisely:

$$f\text{ is surjective}⟺\forall y\in Y,\exists x\in X|f(x)=y$$

600 Here, $f$ is non-surjective because the element $4\in Y$ has no corresponding value in $X$. $g$, however, is surjective, because every element in $Y$ has one or more corresponding elements in $X$.

Bijective §

A bijective function is one that is both injective and surjective. In other words, every element in $Y$ must have one corresponding element in $X$.

Function - Maths _1.excalidraw