Gauss' Law

Gauss’ law is a method to determine the Electric Field for Continuous Charge Distributions, provided they have some degree of symmetry. It uses the concept of Electric Flux and Electric Field Symmetry

Definition §

Gauss' Law ^formula

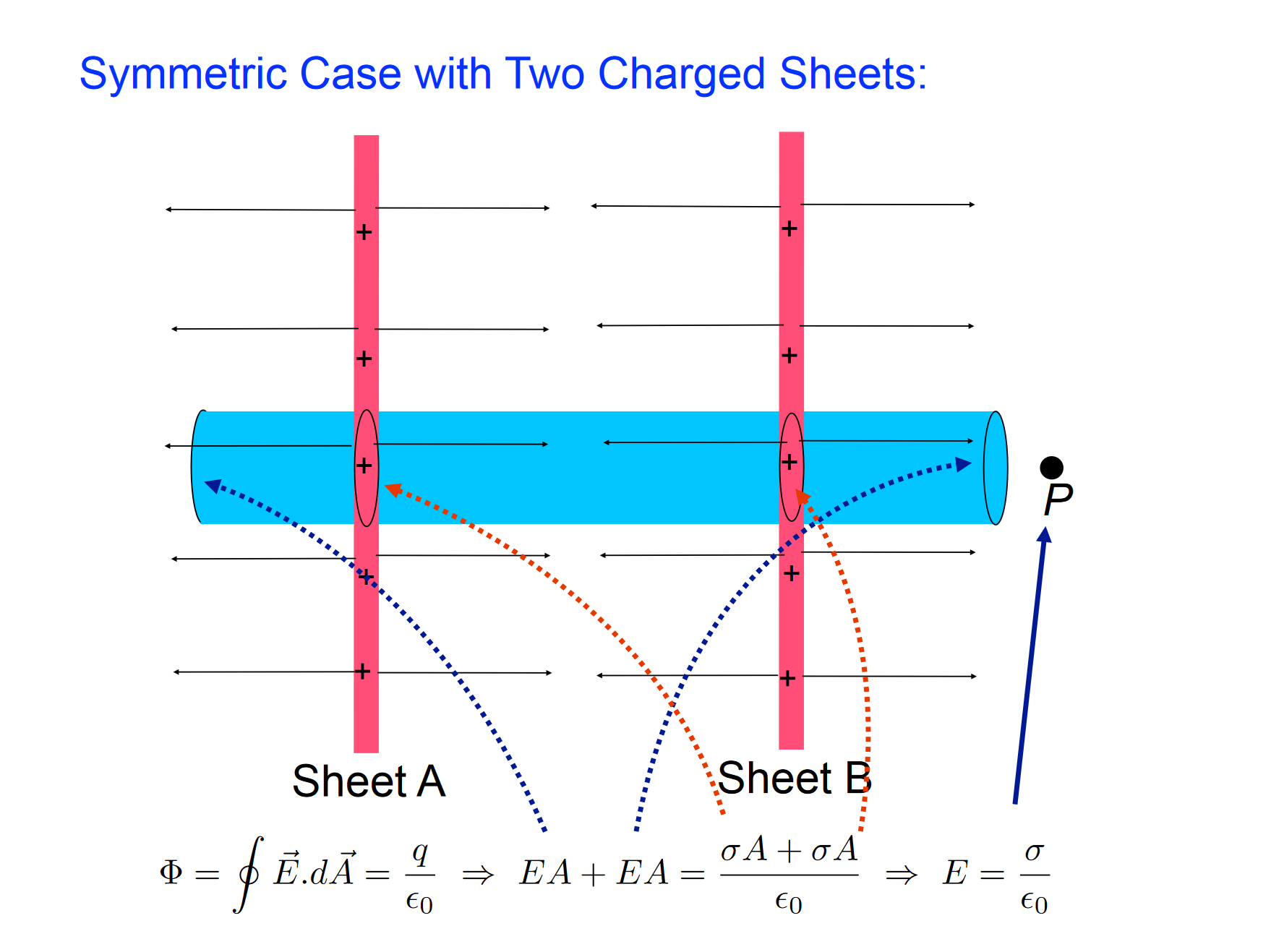
\Phi_{E} = \oint \vec{E} \cdot d\vec{A} = \dfrac{q_{enclosed}}{\epsilon_{0}}

• ${\Phi }_E$ = Electric Flux (in $N/C{m}^2$)
• $\oint$ = Surface Integral
• $\vec{E}$ = Electric Field passing through the Gaussian Surface used to model the object.
• $\vec{A}$ = Area vector of Gaussian surface
• $q$ = Charge Enclosed by the gaussian surface (in $C$)

Applications §

Generally, the goal of Gauss’ Law is to identify either the enclosed Charge or the Electric Field of a charge distribution.

If the Gaussian surface is chosen such that $\vec{E}$ is perpendicular to certain areas vectors , ${\vec{A}}_{\perp }$, and parallel to certain area vectors, ${\vec{A}}_{\parallel }$ (which is the entire goal), then the surface integral can be solved easily. In order to do so, it’s important to know the Electric Field Symmetry of the distribution being solved for.

$\oint d\vec{A}=A$

$$|\vec{E}||{\vec{A}}_{||}|=\frac{q}{{ϵ}_0}\to \vec{E}=\frac{q}{{ϵ}_0|A_{||}|}$$

Generally, we use a finite cylinder or a sphere to act as the gaussian surface.

Superposition §

We can superpose multiple gaussian surfaces (or even just the electrical fields for a single gaussian surface) in order to calculate more complex charge distributions.

#todo

Examples §