Limits

A limit is the value that a mathematical function approaches to as it’s input approaches some value. In other words, it is the value that a function converges to, but does not necessarily equate to. Limits are used to define derivates (using First Principles) and continuity, as well as to find the long-term behaviour of a function

Definition §

Let $f:D\to \mathbb{R}$, where $D$, the domain, is a subset of all real numbers (i.e. a real-valued function). Then:

${\lim }_{x\to a}f(x)=Lifx\ne a$ As x approaches a, f(x) approaches (or converges) to L

Well, that’s a simplified definition. A more formal (and mathematically correct definition) can be found here: Formal Definition of a Limit

Limits must be:

• Unique: There cannot be two limits for a given function at the same point
• Real: Limits must belong to the real set, $\mathbb{R}$
• Finite: While x can approach infinity, the limit of $f(x)$ must be finite i.e. limits can never be infinity

Theorem - Limits from different Sides §

Since limits must be unique, piecewise functions cannot have a defined limit if there are multiple values of the function approaching the same input value, even if they aren’t defined at that input value.

Example

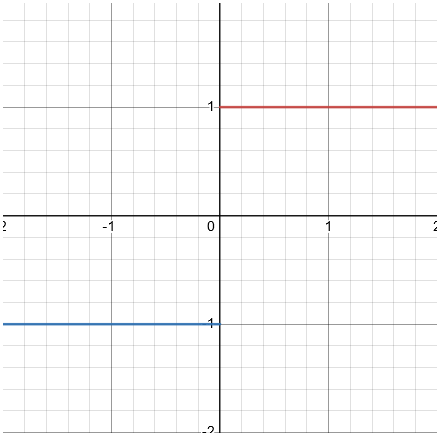
Take the following graph of the function:

$f(x)=\{\begin{array}{ll}1,& x>0\\ -1,& x\le 0\end{array}$

What is ${\lim }_{x\to 0}f(x)$?

As you can see, limits can have different values if the function is approached from the right or left side. Hence, to solve this problem a simple theorem exists:

${\lim }_{x\to a}f(x)=L⟺{\lim }_{x\to a^{-}}f(x)=L={\lim }_{x\to a^{+}}$ In plain words, the limit exists at a point a if, and only if, the right hand and left hand side limits both exist and are equal

Limit Laws §

Limit Laws

1. ${\lim }_{x\to a}[f(x)+g(x)]={\lim }_{x\to a}f(x)+{\lim }_{x\to a}g(x)$
2. ${\lim }_{x\to a}[c\times f(x)]=c\times {\lim }_{x\to a}f(x)$
3. ${\lim }_{x\to a}[f(x)\times g(x)]={\lim }_{x\to a}f(x)\times {\lim }_{x\to a}g(x)$
4. ${\lim }_{x\to a}\left[\frac{f(x)}{g(x)}\right]=\frac{{\lim }_{x\to a}f(x)}{{\lim }_{x\to a}g(x)}if{\lim }_{x\to a}g(x)\ne 0$
5. ${\lim }_{x\to a}c=cifc\ne \infty$
6. ${\lim }_{x\to a}x=aifa\ne \infty$

Link to source

Standard Limits §

Standard Limits

The following limits do need any further proof to be used. Make sure to say that they are standard limits in working out.

1. ${\lim }_{x\to \infty }\frac{1}{x^p}=0,(p>0)$
2. ${\lim }_{x\to \infty }{r}^x=0,(0\le r<1)$

Link to source

Solving Limits As X Approaches Infinity §

There are multiple methods for solving limits as x approaches infinity (since limits cannot equal infinity) that have unique conditions.

Function Form	Technique	Notes
$f(x)=\frac{\infty }{\infty }$ where common terms exist	Divide numerator and denominator by the [[Complexity Analysis#asymptotic-notation	fastest growing term]].
$f(x)=\frac{\infty }{\infty }$ or $\frac{0}{0}$	[[L’Hôpital’s Rule	L’Hôpital’s Rule]]
$f(x)=\infty -\infty$	Multiply and divide by conjugate	If the function is expressed as $a+b$ then it’s conjugate is $a-b$

If all else fails, use the Sandwich Theorem:

Definition §

Let $f(x),g(x),h(x)$ all be real-valued functions that operate over a domain of x, where $x\ne a$:

$Ifg(x)\le f(x)\le h(x)$ $and{\lim }_{x\to a}g(x)=L={\lim }_{x\to a}h(x)$ $then{\lim }_{x\to a}f(x)={\lim }_{x\to a}h(x)={\lim }_{x\to a}g(x)=L$ In other words, if f(x) is strictly bound between g(x) and h(x) over a domain and both limits of g(x) and h(x) exist and are equal, then the limit of f(x) is equal to the limits of g(x) and h(x).

Link to source